5 Tips Excel Hypothesis Testing

Introduction to Hypothesis Testing in Excel

Hypothesis testing is a statistical technique used to make inferences about a population based on a sample of data. It is a crucial tool in data analysis, allowing us to test assumptions and make informed decisions. Excel, being a powerful spreadsheet software, provides various tools and functions to perform hypothesis testing. In this article, we will explore 5 tips for using Excel to perform hypothesis testing.

Understanding the Basics of Hypothesis Testing

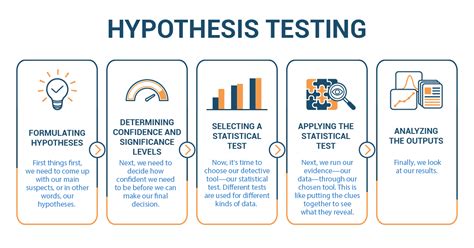
Before we dive into the tips, it’s essential to understand the basics of hypothesis testing. A hypothesis test consists of two hypotheses: the null hypothesis (H0) and the alternative hypothesis (H1). The null hypothesis represents the status quo, while the alternative hypothesis represents the change or effect we are trying to detect. We use a sample of data to calculate a test statistic, which is then compared to a critical value or a p-value to determine whether to reject the null hypothesis.

Tip 1: Use the Built-in Functions

Excel provides several built-in functions for hypothesis testing, such as T.TEST, Z.TEST, and CHISQ.TEST. These functions can be used to perform various types of hypothesis tests, including t-tests, z-tests, and chi-squared tests. For example, the T.TEST function can be used to perform a two-sample t-test to compare the means of two groups.

Tip 2: Create a Hypothesis Testing Template

Creating a hypothesis testing template can save you time and effort in the long run. A template can include the necessary formulas and formatting to perform a hypothesis test, allowing you to simply plug in your data and get the results. You can create a template using Excel’s built-in functions or use add-ins like Analysis ToolPak to perform more complex tests.

Tip 3: Use Descriptive Statistics to Inform Your Test

Descriptive statistics, such as means, medians, and standard deviations, can provide valuable insights into your data and inform your hypothesis test. For example, if you’re performing a t-test to compare the means of two groups, you should first calculate the means and standard deviations of each group to ensure that the data meets the assumptions of the test.

Tip 4: Interpret the Results Correctly

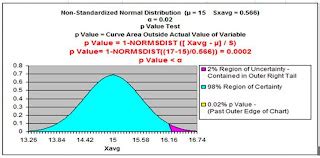
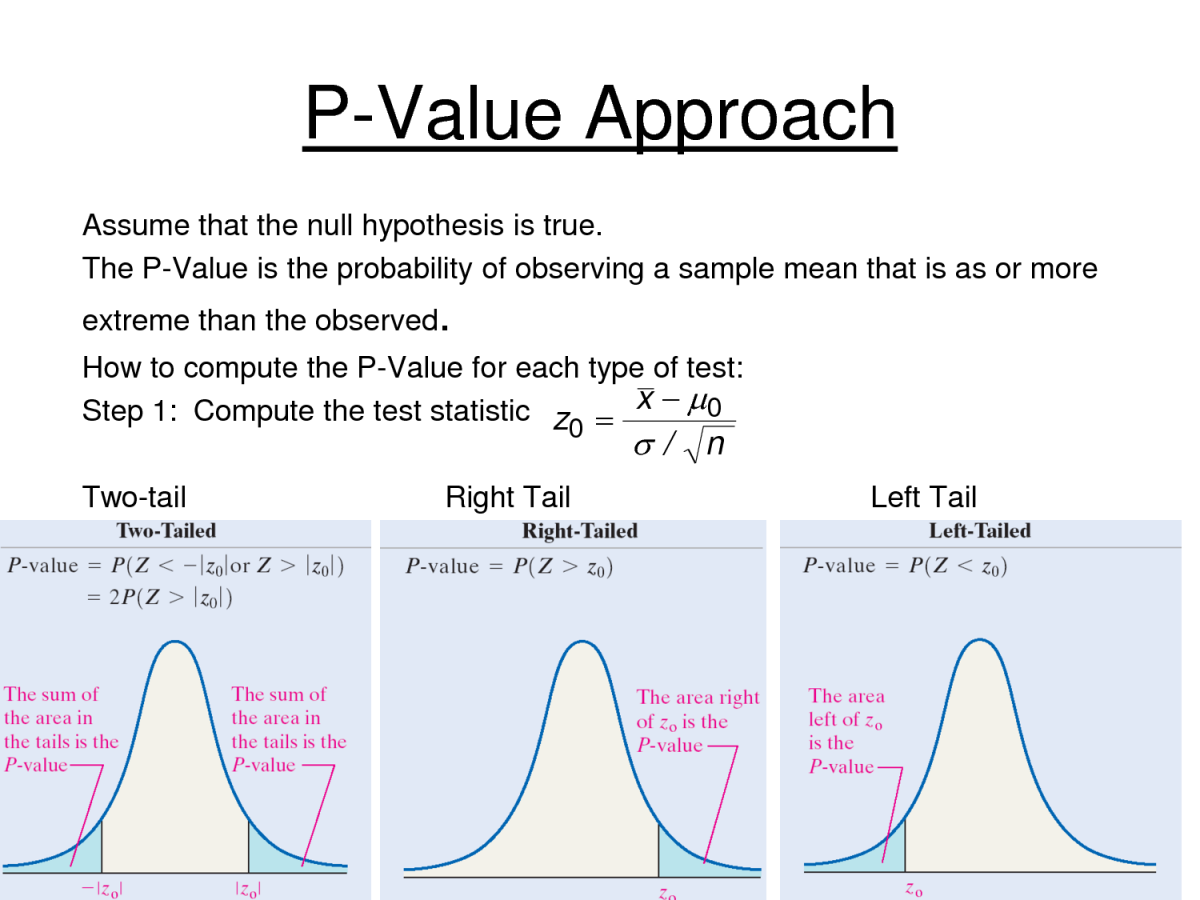
Interpreting the results of a hypothesis test can be tricky, but it’s essential to understand what the results mean. The p-value, for example, represents the probability of observing the test statistic (or a more extreme value) assuming that the null hypothesis is true. If the p-value is below a certain significance level (usually 0.05), we reject the null hypothesis and conclude that the alternative hypothesis is true.

Tip 5: Use Visualization to Communicate Results

Visualization can be a powerful tool for communicating the results of a hypothesis test. Excel provides various visualization tools, such as charts and graphs, that can be used to illustrate the results of a test. For example, a bar chart can be used to compare the means of two groups, while a scatter plot can be used to show the relationship between two variables.

Test	Description	Excel Function
T-test	Compares the means of two groups	T.TEST
Z-test	Compares the mean of a sample to a known population mean	Z.TEST
Chi-squared test	Tests the independence of two categorical variables	CHISQ.TEST

📝 Note: It's essential to choose the correct test based on the research question and the type of data.

In summary, hypothesis testing is a powerful tool for making inferences about a population based on a sample of data. By using Excel’s built-in functions, creating a hypothesis testing template, using descriptive statistics to inform your test, interpreting the results correctly, and using visualization to communicate results, you can perform hypothesis testing with confidence. Remember to choose the correct test based on the research question and the type of data, and to interpret the results correctly to avoid making incorrect conclusions.